Richard Meurman och statistiken

(Obs! Vissa matematiska formler kan se underliga ut i denna html-version om din webbläsare inte är tillräckligt ny. Artikeln finns även i pdf-format. Debatt kring denna artikel finns på denna sida.)

Jesper Jerkert. En doktorsavhandling i arkeologi som lagts fram vid Uppsala universitet visar sig vid närmare granskning lida av både statistiska och geologiska brister.

Richard Meurman disputerade den 14 april 2000 vid Uppsala universitet på den arkeologiska avhandlingen Silverberg i järnbärarland, som – om den vore pålitlig – helt skulle ändra Sala silvergruvas tidigaste historia.¹ Drygt ett år senare publicerades en mycket negativ recension i Fornvännen skriven av geologen Peter Kresten.² Jag bestämde mig för att själv läsa avhandlingen för att försöka bilda mig en egen uppfattning. I denna artikel redovisar jag vad jag har funnit. Medan Kresten levererade övergripande kritik som handlar ungefär lika mycket om statistik som geologi, kommer jag speciellt att inrikta mig på statistiken i avhandlingen. Geologi kommer endast att diskuteras översiktligt.

Schmidthammaren

Richard Meurmans avhandling handlar om hur man med hjälp av ett mekaniskt instrument, Schmidthammaren,³ ska kunna fastställa övergivna gruvors och gruvhåls ålder. Hammaren uppfanns 1948 för mätning av hårdheten hos betong. En tyngd får med hjälp av en fjäder slå till mot en kolv vars andra ände är i kontakt med det undersökta underlaget. Tyngdens återstuds registreras på en skala från 10 till 100 och kallas R-värde (rebound). R-värdet anses vara proportionellt mot hårdheten, som i sin tur antas vara proportionell mot graden av vittring.

Vittringen är slutligen enligt Meurman linjärt beroende av tiden, dvs. av hur länge sedan stenytan blottlades. Genom att jämföra R-värdena som erhålls vid slag på den vittrade bergytan med värdena för slag på en färsk yta (som alltså inte har hunnit vittra), menar Meurman att han kan datera den vittrade ytan. Närmare bestämt så görs en serie om ca 15-20 slag med hammaren på var och en av ytorna. De genomsnittliga R-värdena för vittrad respektive ovittrad yta räknas ut, och skillnaden mellan dem kallas D-värde (differens). Det är alltså D-värdet som Meurman anser vara direkt proportionellt mot den vittrade ytans ålder.

De enskilda R-värdena varierar ganska mycket, men det är inget som i sig misstänkliggör hela metoden. Bergytor är sällan speciellt homogena, utan har både hårdare och mjukare beståndsdelar. (Olika bergarter har förstås olika sammansättning i detta avseende.) Eftersom hammarslagen påverkar ytan görs de inte på exakt samma ställe.

Kalibreringslinjen

Av central betydelse för Meurmans metod är att man kan fastställa en kalibreringsskala, ett matematiskt samband som gör det möjligt att översätta varje D-värde till en ålder. För ändamålet fastställer Meurman D-värden för 18 gruvlämningar med mer eller mindre känd ålder. Resultaten återges i figur 1.⁴ Det ser ut att vara ett starkt linjärt samband.⁵ Ändå är Meurman inte nöjd. Han förkastar 16 av punkterna och behåller endast två. Med hjälp av dessa två punkter, för åren 1623 och 1686, plus origo (år 2000), konstruerar han sin kalibreringslinje. Meurmans skäl för att förkasta 16 punkter är att de historiska dateringarna är osäkra. Endast dateringarna från 1623 och 1686 är helt säkra med hänsyn till de skriftliga källorna, anser han. Detta är å ena sidan ett fullt förståeligt resonemang som visar på en vilja till hård källkritik. Å andra sidan är det en smula märkligt att slänga bort så många mätpunkter som passar så väl in i ett linjärt samband. Felmarginalen för dateringar blir nämligen i allmänhet större om kalibreringslinjen bygger på färre mätpunkter. Detta är dock inget som Meurman diskuterar.

Figur 1. De ursprungliga 18 kalibreringspunkterna. Åldern 0 (noll) motsvarar år 2000. Data till figuren har hämtats ur doktorsavhandlingens tabell och figur på s. 71. På s. 69 finns en tabell med samma uppgifter. Där finns dock flera skillnader gentemot s. 71, bl.a. att två årtal, 1852 och 1858, har bytt D-värden med varandra.

Och ännu märkligare blir det om man tittar närmare på Meurmans resonemang om de yngsta dateringarna. Man borde förvänta sig att dessa, särskilt de från 1900-talet, skulle vara de säkraste när det gäller de skriftliga källorna. Ändå ligger inte dessa punkter närmare en inritad regressionslinje än de äldre punkterna, snarare tvärtom.⁶ Figur 2 visar samma sak som figur 1, men med en av mig inritad regressionslinje, och med de sex yngsta punkterna numrerade 13-18. Här syns tydligt att det är flera av de yngsta punkterna som avviker mest. Detta bekymrar Meurman, som talar om ”starkt avvikande värden” bland de sex yngsta dateringarna. Karakteristiken är enligt min mening överdriven – jag tycker inte att det finns några starkt avvikande värden i figur 2. Om de sex yngsta punkterna skriver han också att ”[t]re av ST-dateringarna ligger nära trendlinjen medan de övriga tre ligger längre ifrån linjen”.⁷ Jag tycker att det är svårt att med blotta ögat avgöra vilka punkter Meurman syftar på.⁸ Det framgår av avhandlingen att nr 18 är en av de avvikande punkterna. De andra två har jag fått reda på är nr 13 och 16.⁹ Meurman lanserar en förklaring till varför vissa yngre punkter avviker. Jag ska inte försöka avgöra om förklaringen verkar rimlig. Däremot finns en del att säga om Meurmans metod när han påstår att tre punkter ligger nära linjen och tre ligger längre bort.

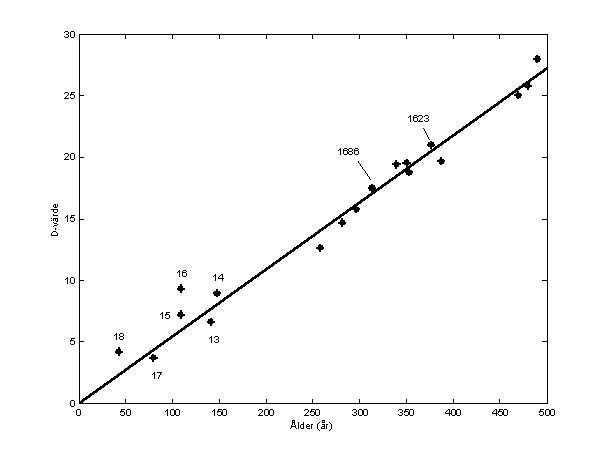
Figur 2. De 18 kalibreringspunkterna med regressionslinje inritad enligt minsta kvadrat-metoden. Linjen har tvingats gå genom origo. De sex yngsta punkterna har numrerats. De punkter som motsvarar 1623 och 1686 har markerats.

Den normala metoden för att bedöma en punkts avvikelse från en regressionslinje är att mäta avståndet i y-led. Med denna metod, och med linjen dragen på gängse sätt (se nedan), blir punkterna 16, 18 och 15 (inte 13) de mest avvikande, i tur och ordning. Men Meurmans metod att bedöma punkternas avvikelse från linjen är av allt att döma istället att beräkna hur mycket inversen av lutningen för linjer dragna från origo till punkterna skiljer sig från trendlinjens inversa lutning. (Se nedan om varför Meurman är intresserad av lutningens invers.) Denna metod skulle i många leda fall till ytterst bisarra konsekvenser, vilket kan konstateras i figur 3. Meurmans metod återfinns inte i någon statistisk lärobok, och den är uppenbart olämplig.

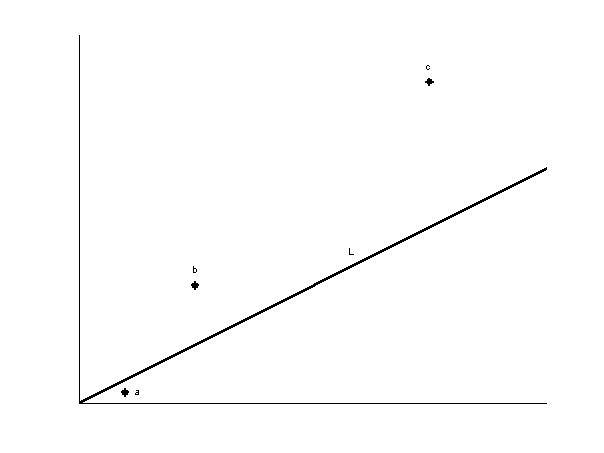
Figur 3. Med Meurmans metod skulle punkten b avvika mer från linjen L än punkten c. Allra mest skulle dock a avvika! Naturligtvis avviker c mest enligt gängse sätt att mäta, följt av b och sist a.

Jag ska återkomma till de 18 ursprungliga kalibreringspunkterna senare, men låt oss nu gå vidare. Vi har alltså kastat bort 16 punkter och har två kvar, plus origo. Hur anpassar man en rät linje till dessa? Det finns en metod, som kallas minsta kvadrat-metoden (MK-metoden). Den går ut på att minimera summan av kvadraterna på avvikelserna i y-led. MK-metoden har flera önskvärda egenskaper, och är helt dominerande när det gäller anpassning av matematiska samband till empiriska data.¹⁰ Om man vill använda någon annan metod bör man därför motivera detta väl. Meurman använder dock utan förklaring en hemmagjord metod för att räkna ut linjens lutningskoefficient k.¹¹ Fortsättningsvis är han mest intresserad av inversen till k, varför han definierar den s.k. bergsmultiplikatorn B (eller Bm) som B = 1/k. Bergsmultiplikatorn anger det antal år som motsvarar ett D. Om en hammardatering ger ett slutligt D-värde på x, så ska den vittrade ytan alltså vara B^.x år gammal.

Man kan tycka att det inte spelar så stor roll vilken metod Meurman använt, eftersom de tre punkterna – för år 1623, 1686 och 2000 – ligger på så gott som rät linje. Men det är konstigt att ingen i Meurmans omgivning påpekat det olämpliga i att använda en egen metod när man kan slå upp vilken metod som rekommenderas i en godtycklig lärobok i statistik. Den person som först av alla borde ha reagerat hittade faktiskt på metoden, enligt Meurman: ”Det är min handledare Frands Herschend som har introducerat detta sätt att räkna ut Bm. Så vitt jag vet är detta det mest relevanta sättet att beräkna Bm.”¹²

Redan att de tre valda punkterna ligger på nästan exakt rät linje är i sig ägnat att väcka misstankar. Om en av punkterna, den från 1623, skriver Meurman: ”Ytan är lätt att återfinna och flera ST-dateringar har gjorts och den som ger det bästa värdet har D. 20,95”.¹³ Jag har frågat vad han menar med ”det bästa värdet”. Han svarade: ”Eftersom det här är en tvärvetenskaplig metod för relativa dateringar som bygger på historiskt källmaterial, är det logiskt att använda det mätvärde/D (differens) som ligger närmast den historiska uppgiften.”¹⁴ Svaret är förbryllande och samtidigt mycket avslöjande. Man kan ju inte avgöra vilken ålder ett visst D-värde motsvarar utan att ha en kalibreringslinje. Och kalibreringslinjen kan man inte räkna ut förrän man har bestämt vilka punkter man ska anpassa den till. Men en av de punkter som bestämmer linjens ekvation är just D-värdet för år 1623. Meurman har alltså gjort en åldersbestämning med hjälp av en ännu icke existerande kalibreringslinje! Jag har i en uppföljningsfråga undrat vilken metod Meurman har använt för att datera värdet D. 20,95. Meurman har inte givit något tillfredsställande svar, utan skriver att han tycker att ”det är uppenbart hur jag kommit fram till detta”.¹⁵ Svaret ger intrycket att Meurman inte inser att här finns ett problem.

Det finns ingen möjlighet att utan en kalibreringslinje avgöra vilken av hammardateringarna för år 1623 ”som ligger närmast den historiska uppgiften”. Meurman har alltså inte lyckats förklara hur kalibreringslinjen tillkommit.

Fler fel

Jag har uppehållit mig länge vid kalibreringsskalan, eftersom den har avgörande betydelse för Meurmans metod. Avhandlingen innehåller även mer traditionella fel, stora som små.¹⁶

Det finns dock ytterligare ett statistiskt resonemang som måste beröras. På s. 71-73 utreder Meurman vilket antal slag som är lämpligt i varje serie. Han har gjort några längre serier, oklart hur många, om 40, 80 eller 100 slag. Tyvärr utnyttjar han inte hela detta material för analys. Istället drar han av allt att döma sina slutsatser om det optimala antalet slag utifrån endast två serier om 100 slag, som är avbildade i två spridningsdiagram på s. 73. Det verkar som om han bara har tittat i diagrammen och dragit slutsatser efter vad han tycker sig ha sett.¹⁷ Jag återger i figur 4 en av de två analyserade slagserierna. Meurman skriver om denna: ”Efter ca 20 till 25 slag sjunker differenserna påtagligt, för att mellan 40 till 60 slag åter stiga till samma förhållande som mellan 1 till 20 slag. Mellan 70 till 90 slag sjunker värdena ner mot 30 D. och även under det. Från 90 till 100 slag stiger värdena åter upp mot 45 till 55 D.”¹⁸ Därefter följer en noggrann geologisk förklaring till beteendet. Men underlaget verkar vara alldeles för litet för att tillåta slutsatser av denna typ, och om man ändå vill dra sådana måste man utföra statistiska tester på materialet. Det räcker inte att titta i figurer.

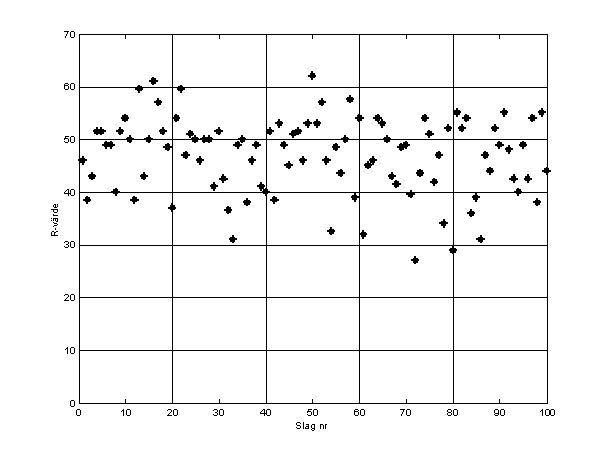
Figur 4. En återgivning av fig 23 på s. 73 i Meurmans avhandling. Just denna slagserie är gjord på färsk (ovittrad) yta.

Hur stor är osäkerheten?

En oerhört viktig fråga angående Meurmans metod är förstås: Hur stor är felmarginalen i dateringarna? Det är mycket märkligt att denna fråga inte diskuteras i avhandlingen. Däremot har Meurman i andra sammanhang angivit vissa ungefärliga felmarginaler. I en artikel i UNT hävdar han att metoden är enklare och mer användbar än kol-14-datering, vilket torde innebära en mycket god dateringsprecision.¹⁹ Han ska ha framfört en liknande åsikt på ett föredrag hos Jernkontoret.²⁰ I CD-uppsatsen skriver han att felmarginalen är ca ±60 år.²¹ I en annan artikel i UNT anges felmarginalen till ±30 år.²² I VLT uppges felmarginalen vara ±40 år.²³ Sammantaget tycks alltså Meurman anse att hans metod har en felmarginal på ungefär ±30-60 år. Om det stämmer är det en utomordentligt bra siffra. Det är bara förvånande att han ingenstans i doktorsavhandlingen har räknat ut den.

Men vi ska räkna! Eftersom vi vet att en av punkterna (den från 1623) som ligger till grund för Meurmans kalibreringslinje är felaktig, är det ingen större mening med att räkna ut felmarginalen utifrån denna linje. Intressantare är att beräkna felmarginalen för en linje som anpassas till de 18 ursprungliga kalibreringspunkterna. Felmarginalen blir då ca ±60 år (95% konfidensintervall).²⁴ Detta överensstämmer ungefär med vad Meurman har sagt. Så vad är problemet?

Uppfyllda förväntningar

Det finns såvitt jag kan se ytterligare två problem med de ursprungliga 18 kalibreringspunkterna. Det första är att många av dateringspunkterna helt uppenbart motsvarar Meurmans förväntningar, därtill med osedvanligt god precision. Medan Meurman själv, som vi har sett, anser att flera av de 18 ursprungspunkterna avviker störande mycket för att tas med i beräkningen av regressionslinjen, är min åsikt, som säkert framgått, den motsatta: Resultaten är lite för bra för att verka helt trovärdiga, särskilt när det gäller de äldre punkterna, och särskilt med tanke på att Schmidthammaren allmänt anses vara en grov mätmetod (se nedan).

Kan vi vara säkra på att Meurman inte har förfarit med flera av de 18 punkterna precis på samma sätt som med punkten för 1623, alltså att han har haft flera värden att välja mellan och att han har valt det som bäst uppfyllde hans förväntningar? Åtminstone kan han ha gjort så med vissa andra punkter som ej ingår bland de 18 – han skriver på ett ställe att han valt ”det mest pålitliga värdet” och ”ett representativt medelgradvärde”, utan att precisera vad dessa begrepp betyder.²⁵ Rent allmänt om provtagning i fält skriver han också: ”På ett relativt tidigt stadium uppstod en del ’konstigheter’ i samband med dateringarna. Detta gällde i första hand de historiskt daterade gruvorna. Vid omslag av serier visade det sig att vittringsvärdena kunde skilja sig en hel del och därigenom ge olika dateringar.”²⁶ Meurman ger dessa avvikelser en geologisk förklaring i form av dolda sprickbildningar i berget. Om olika serier ger olika resultat beroende på att vissa serier påverkats av dolda sprickbildningar, så är detta något som jag föreställer mig skulle kräva ganska mycket arbete för att leda i bevis. Men Meurman meddelar bara på två rader att det rör sig om sprickbildningar, och det är omöjligt att avgöra hur pass säker denna förklaring är.

Det är inte bara D-värdena i sig som stämmer bra överens med förväntningar. Hela Meurmans arbete tycks vara frukten av en önskan att bekräfta gamla sägner som berättar om Sala silvergruvas tidigaste historia. I avhandlingen heter det: ”Det fanns ett antal sägner och legender som berättade att silver skulle ha börjat utvinnas redan på 1100-1200-talen i området norr om det egentliga Storgruveområdet. (…) Ett beslut växte fram hos mig att försöka ta reda på om traditionerna kunde rymma en kärna av sanning. (…) Således började jag läsa arkeologi vid Uppsala universitet våren 1993 för att på så sätt kunna börja med en undersökning som, förhoppningsvis, skulle leda fram till att gåtan med Sala gruvas ålder kunde få en lösning.”²⁷ En ännu tydligare formulering finns i en annan artikel: ”Jag började läsa arkeologi vid Uppsala universitet 1993 bland annat för att kunna hitta en arkeologisk metod för att kunna bevisa det jag trodde beträffande Sala silvergruvas ålder.”²⁸ Med tanke på denna inställning, och på hur väl dateringarna bekräftat förväntningarna, vore det bra om Schmidthammarens dateringsförmåga kunde prövas i ett strikt blindtest.

Det andra problemet med de 18 punkterna är att de tyder på en mycket större noggrannhet hos Schmidthammaren än vad som är allmänt erkänd. Jag ska nu kommentera detta och de geologiska antagandena.

Schmidthammaren och geologin

Schmidthammaren anses vara ett mätinstrument som endast ger grova uppskattningar. Detta har jag fått bekräftat av en betongexpert och två geologer, vilka samtliga har erfarenhet av hammaren. De uttryckte skepsis över möjligheterna att använda hammaren till dateringsändamål på Meurmans vis.²⁹ Enbart skepsis räcker förstås inte för att avfärda hammaren, men Meurman borde nog ha behandlat de avvikande åsikterna lite mer. Han citerar till och med själv i sin avhandling en geolog, Johan Holmgren, som anser att hammaren är en ”grov mätmetod”.³⁰

Är vittring av bergytor verkligen linjär mot tiden? Geologen Runo Löfvendahl, som arbetat mycket med vittringsfrågor, anser inte det. Han framhåller att vittring är ett mångfasetterat begrepp, som inbegriper bl.a. kemisk vittring (t.ex. att olika mineral upplöses olika fort av regnvatten), biologisk kolonisering i form av alger och lavar, plötsliga förlopp i form av frostsprängning och liknande, samt eventuell påverkan från människan och andra djur. Möjligen, anser Löfvendahl, kan vittringen betraktas som approximativt linjär i kanske några hundra år (beroende på bergart och yttre omständigheter). Därefter är vittringen mera episodisk med rena materialförluster pga. frys-/töcykler, saltsprängning eller större temperaturvariationer. Det är dock extra svårt att säga något allmängiltigt om vittringsbeteendet i en så speciell miljö som en gruva.³¹

Att Meurman varit åtminstone ytligt medveten om sådana problem framgår redan i hans CD-uppsats: ”En återstående fråga är hur långt tillbaka i tiden dateringarna kan komma. Eftersom bergets vittring till slut blir så stor att stenen faller sönder så ökar felmarginalen ju längre tillbaka man kommer.”³² Även i doktorsavhandlingen noterar Meurman i förbigående (s. 22) att vittring på berghällar enligt en refererad rapport inte anses linjär på långa tidsskalor. Ändå redovisar han dateringar ända tillbaka till 1000-talet. Det framgår inte hur han har kommit fram till att vittringen trots allt är linjär under så lång tid. Han skriver bara kort: ”Beträffande vittringen kan sägas att den, efter preliminär beräkning, efter ca 1000 år blir så stor att ytan faller sönder och omöjliggör ST-dateringar.”³³ I ett inlägg i dagspressen har han som svar på kritik skrivit att ”[m]ina forskningsrön visar tvärtemot att vittringen är näst intill linjär”.³⁴ Om Meurman sitter inne med forskningsrön kring vittring som inte nämnts i avhandlingen bör han presentera dem. Att han lyckats datera en mängd gruvor med stor noggrannhet under antagandet om linjär vittring räcker inte som argument, eftersom dateringarna kan ifrågasättas på statistiska grunder och av förväntansskäl. Vad som krävs är goda argument som är oberoende av Schmidthammardateringarna.

Hur kan man vara säker på att ytan man slår på inte är resultatet av en frostsprängning flera hundra år efter gruvans förmodade ursprungsålder? Meurman är medveten om problemet (s. 78), men behandlar det ytterst kortfattat.

Andra möjliga felkällor är påverkan från omgivningen. Dateringarna görs ju i gruvöppningar eller i gruvhål som ligger helt öppna för väder och vind. Borde det då inte spela roll om bergväggen man daterar vetter åt norr eller söder? Spelar det ingen roll hur naturen runt omkring ser ut? Är det oväsentligt att berget en gång kan ha brutits med hjälp av tillmakning (upphettning med hjälp av brasor och därefter snabb kylning med hjälp av vatten) medan färskytorna slås fram på annat sätt? Har inte långsiktiga klimatförändringar någon betydelse? Kan inte luften i gruvområdet ha innehållit betydligt mer föroreningar under den mest intensiva brytningsperioden än idag, och borde inte det ha påverkat vittringshastigheten? Även Peter Kresten har rest några av dessa invändningar i sin recension.

Diskussion

Jag har inte tillräckliga geologiska kunskaper för att definitivt kunna avfärda Schmidthammaren som dateringsinstrument, men de uppgifter jag har fått fram inger mig starkt tvivel. Det vore önskvärt om fler geologer kunde yttra sig om Meurmans vittringsantaganden. Om möjligt vore det också bra med blindtestning av hammaren, dvs. åldersbestämning där det finns en historiskt fastslagen ålder som handhavaren inte känner till. Att Meurmans metod utsätts för fortsatt kritisk granskning är viktigt inte minst eftersom den anses kullkasta tidigare historieskrivning avseende Sala silvergruva,³⁵ och eftersom Meurman efter sin disputation har fortsatt att använda hammaren och tycks nå kontroversiella resultat.³⁶

Oavsett Schmidthammarens framtida öde inom arkeologin så står det klart att Richard Meurmans doktorsavhandling innehåller några allvarliga statistiska fel. Jag tänker då främst på selektionen av data till kalibreringslinjen, och på de påhittade metoderna för att räkna ut kalibreringslinjens lutning, för att bedöma avvikelser från linjen, och för att bedöma optimala antalet slag i en slagserie. E-postkorrespondensen jag har haft med Meurman tyder på att han inte förstår, eller inte vill erkänna att han förstår, att hans användning av matematik och statistik överhuvudtaget är problematisk.

Icke desto mindre godkändes Silverberg i järnbärarland. Allmänt kan man konstatera att avhandlingen uppfyller åtminstone två av de kännetecken som ofta vidlåder tveksamma avhandlingar.³⁷ För det första befinner sig avhandlingen på gränsen mellan två akademiska discipliner, här arkeologi och geologi. Sådana gränsöverskridande arbeten kan ge många intressanta resultat, men en förutsättning är att forskaren är kunnig i båda ämnena. Meurmans avhandling lades fram i arkeologi, men han tycks inte ha fått tillräcklig handledning i det främmande ämnet geologi. För det andra missbrukas statistik. De statistiska misstagen är dock inte av den kanske vanligaste typen, som innebär en oförmåga att kunna skilja mellan slumpmässiga och troligen icke slumpmässiga samband. I detta fall handlar det om mer grundläggande fel, att Meurman använder hemmagjorda statistiska metoder och att han överhuvudtaget verkar obekant med elementär matematisk statistik.

Den statistiska granskningen av avhandlingen har uppenbarligen inte fungerat. I förordet tackas två professorer i teoretisk fysik, Olle och Nanny Fröman, för statistisk granskning. Olle Fröman, som gjorde den mesta granskningen, har meddelat mig att han tillsammans med en professor i matematisk statistik bedömde den statistiska analysen vara ”helt adekvat”.³⁸ Att den statistiska behandlingen är långt ifrån adekvat hoppas jag ha visat i denna artikel.

Såvitt jag förstår hade inte Meurmans fakultetsopponent, professor emerita i arkeologi Birgit Arrhenius, några större invändningar vid disputationen. Hon har beskrivit avhandlingen som ”en stor framgång”.³⁹ I betygskommittén satt tre arkeologer, varav en hade arbetat mycket med frågor som berör även geologi. Denna person, fil. dr Eva Hjärthner-Holdar, föreståndare för Geoarkeologiska Laboratoriet i Uppsala, reserverade sig mot att godkänna avhandlingen. Hon ansåg att både den statistiska och geologiska behandlingen var otillfredsställande.⁴⁰ Avhandlingen godkändes således med två tredjedelars majoritet.

I slutändan måste en stor del av ansvaret för att Silverberg i järnbärarland publicerats i nuvarande skick läggas på handledaren Frands Herschend. Herschend inte bara hittade på en av de felaktiga statistiska metoderna, utan var också den som från början föreslog att Schmidthammaren skulle användas.⁴¹ Han handledde Meurman redan på CD-nivån. Utan Herschends förtroende för metoden hade det knappast blivit någon avhandling.

Trots att de ansvariga kan identifieras så kan jag inte besvara den kanske intressantaste frågan: Hur har alla dessa misstag kunnat passera?

Noter

Richard Meurman: Silverberg i järnbärarland. Bergshanteringens begynnelse i ljuset av Schmidt Testhammardateringar. Diss., Institutionen för arkeologi och antik historia, Uppsala universitet, 2000.
Peter Kresten: Recension av Silverberg i järnbärarland, Fornvännen 2/2001, s. 140-142.
Meurman skriver ”Schmidt Testhammare” (förkortat ST), men jag kommer att skriva ”Schmidthammare”.
I denna artikel är figur 1 och 2 ritade så att origo är år 2000 och högre x-värden betyder att man går bakåt i tiden. Meurmans originalfigurer är ritade på ett annat sätt.
Korrelationskoefficienten är 0,988.
Å andra sidan är de flesta av de äldre punkterna inte lika säkert historiskt daterade, dvs. det finns en osäkerhet i x-led. Med tanke på detta kan man tycka att Meurman borde visa större tolerans mot att flera av de yngre punkterna avviker i y-led.
Båda citaten ur Silverberg i järnbärarland, s. 69.
Ett problem när det gäller diskussionen om hur mycket punkterna avviker från ”trendlinjen” är att Meurman aldrig ritar ut någon sådan linje som är anpassad till alla 18 punkterna. Linjen som finns i figur 2 har jag anpassat med hjälp av minsta kvadrat-metoden. Jag har tvingat linjen att gå genom origo, eftersom Meurman gör så med den linje han till slut fastnar för. Meurman använder en egen metod för att dra linjen. Min linje i figur 2 avviker ytterst lite från Meurmans slutliga linje.
E-post från Richard Meurman till Jesper Jerkert 2001-12-18. Den kompletta korrespondensen mellan mig och Meurman kan erhållas på begäran.
MK-metoden och dess goda egenskaper finns beskrivna i många läroböcker. Jag rekommenderar Göran Andersson, Ulf Jorner & Anders Ågren: Regressions- och tidsserieanalys med och utan datorstöd. Lund: Studentlitteratur, 1994, 2:a uppl., s. 28-34.
Silverberg i järnbärarland, s. 70. Meurman använder formeln k = Σy_i / Σx_i. Korrekt enligt MK-metoden, om man vill att linjen ska gå genom origo, vore k = Sigma;x_iy_i / Sigma;x_i².
E-post från Richard Meurman till Jesper Jerkert 2001-12-18.
Silverberg i järnbärarland, s. 70.
E-post från Richard Meurman till Jesper Jerkert 2001-11-08.
E-post från Richard Meurman till Jesper Jerkert 2001-12-18.
Några exempel: Minst tre av de sex figurerna som täcker sidorna 74-75 innehåller fel. På s. 12 anges Schmidthammarens skala motsvara återstudsens distans i procent av slagkolvens framåtrörelse. En procentangivelse kan inte ha någon enhet. Icke desto mindre uppges på s. 61 skalans enhet vara Newtonmillimeter – och dessutom tycks Newtonmillimeter kunna förkortas såväl Nmm² som Nm² (s. 61 resp. 174; båda är fel). Någon erratalista som rättar fel av denna typ har inte publicerats. (E-post från Richard Meurman till Jesper Jerkert 2001-12-18.)
Jag har frågat Meurman om han endast har använt två serier om 100 slag som grund för sin analys. Han har svarat att all information jag behöver finns på s. 73 i avhandlingen (e-post 2001-12-18). Men där står inget om några fler serier, varför jag drar slutsatsen att han verkligen bara använt två serier.
Silverberg i järnbärarland, s. 73. Såvitt jag förstår ska enheten på y-axeln inte vara D, som Meurman skriver, utan R, alltså de enskilda slagens återstudsvärde.
Hans Lundgren: ”Kritiserad avhandling: Metoden omstridd bland forskarna”, Upsala Nya Tidning 2001-10-01.
E-post från Peter Kresten till Jesper Jerkert 2001-11-14.
Richard Meurman: Medeltida Salasilver. Schmidt Testhammare som dateringsinstrument. CD-uppsats, Institutionen för arkeologi och antik historia, Uppsala universitet 1994, s. 57. Resonemanget lyder som följer: ”Vad slutligen gäller testhammarens felmarginaler så har det visat sig att standardavvikelsen är maximalt 2,5 Enheter. Då en Enhet motsvarar ca. 18 år så är plus-minusförskjutningen i tid ungefär 60 år. Detta gör att ’träffsäkerheten’ vid dateringar är god.” Standardavvikelsen som Meurman diskuterar här är den för enskilda slag i en slagserie jämfört med seriens genomsnitt. Den standardavvikelsen är inte relevant i sammanhanget.
Hans Lundgren: ”Silver bröts i Sala redan på 1100-talet: Sensationella uppgifter i avhandling”, Upsala Nya Tidning 1998-01-29, s. 11.
Olle Stenberg: ”Han hamrade fram gruvans ålder”, Vestmanlands Läns Tidning 2000-05-04, s. 8.
Felmarginalen är lite olika stor beroende på hur gammal dateringen är. Peter Kresten uppger i sin recension att felmarginalen skulle vara betydligt större, men han har utgått från standardavvikelsen för enskilda slag, vilket inte är korrekt. Felmarginalen ges i själva verket av uttrycket 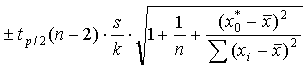, där 1-p anger konfidensgraden (för 95% konfidens alltså p = 0,05), t_p/2(n-2) är ett tal ur t-fördelningen som kan avläsas i tabell, n är antalet punkter som linjen grundas på (här alltså n = 18), s är punkternas standardavvikelse från regressionslinjen, k är en MK-skattning av linjens lutningskoefficient och x₀* är mittpunkten i konfidensintervallet (här alltså en punktskattning av åldern för den gruva man är intresserad av). Att denna formel är den korrekta har bekräftats av Jan Enger och Gunnar Englund, båda universitetslektorer i matematisk statistik, KTH.
Silverberg i järnbärarland, s. 67.
Silverberg i järnbärarland, s. 64.
Silverberg i järnbärarland, s. 9.
Richard Meurman: ”Schmidt Testhammare – en ny dateringsmetod som gjort Sala silvergruva äldre”, Sala Hembygds- och Fornminnesförening. Årsbok, årg. 45, 1994, s. 12.
Samtal med ingenjör Lennart Törnblom på Cement och Betong Institutet (CBI), 2001-11-12. Telefonsamtal med Ove Stephansson, professor i teknisk geologi, KTH, 2001-11-13. Telefonsamtal med Christopher Talbot, professor i tektonik och geodynamik, Uppsala universitet, 2001-11-14.
Silverberg i järnbärarland, s. 59.
Telefonsamtal med Runo Löfvendahl på Riksantikvarieämbetet 2001-11-13. Se även KLB [Karna Lidmar-Bergström]: ”Vittring”, Nationalencyklopedin bd 20, 1996, s. 10.
Medeltida Salasilver, s. 57.
Silverberg i järnbärarland, s. 78.
Richard Meurman: ”Genmäle på kritiserad avhandling”, Upsala Nya Tidning 2001-11-26, s. 11.
Detta har skildrats i en artikelserie av Kent Karlsson i Sala Allehanda, 2001-02-09 – 2001-03-19. Artiklarna finns samlade och utgivna som särtryck: https://libris.kb.se/bib/8572668. Sala silvergruvas nya historia. Sala: Braingress/Sala Allehanda, 2001.
Hans Lundgren: ”Sveriges första järngruvor låg i Uppland: Enligt omstridd forskningsmetod bröts järn i Vattholma redan på 600-talet”, Upsala Nya Tidning 2001-10-01.
Sådana kännetecken diskuteras i Sven Ove Hansson & Per Sandin (red.): Högskolans lågvattenmärken. Stockholm: Natur & Kultur, 2000. Se särskilt Sven Ove Hanssons kapitel ”Vad gick snett?”, s. 285-294.
E-post från Olle Fröman, förmedlat av Nanny Fröman, till Jesper Jerkert 2001-11-04. Jag har frågat vem professorn i matematisk statistik var, dock utan att få något svar.
Sala silvergruvas nya historia, s. 29.
Telefonsamtal 2001-12-03.
Silverberg i järnbärarland, s. 9.