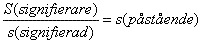Matematikmissbruk

Publicerat i Folkvett nr 4/2006.

Kimmo Eriksson, professor i matematik vid Mälardalens högskola, diskuterar fällorna med att använda matematik i kosmetiskt syfte och utan djupare förståelse.

Ingen kan ha undgått att det är kris i svensk skolmatematik. Samtidigt visar debatten något glädjande: i alla läger är man enig om hur angeläget det är med god matematikundervisning. Ämnet åtnjuter ett anseende som är få andra förunnat. Hur kan det komma sig? Någon särskild status kan ju knappast härledas från oss yrkesmatematiker, med vårt solida rykte som illa klädda enstöringar.

Matematikens anseende kommer istället från en annan källa – vetenskapen. Att vi utvecklat matematik som kan användas för att beskriva världen är en av mänsklighetens främsta bedrifter. Vetenskapsmän som Arkimedes, Newton och Einstein utvecklade ny matematik för omedelbar tillämpning. När matematiska begrepp och metoder en gång har utvecklats finns de fortsatt tillgängliga för forskare att återanvända på nya problem. Det finns flera potentiella vinster med att använda matematik när man resonerar om världen:

Större precision blir möjlig.
Man tvingas till entydiga definitioner av begrepp, vilket främjar förståelse.
En matematisk modell är lättare att analysera.

Inom vetenskapen vill man ofta undersöka subtila och komplexa ting. Ökade möjligheter till precision, förståelse och analys har då mycket stort värde. Mycket riktigt är matematiska modeller en självklarhet i stora delar av forskarvärlden. Därmed associeras matematik med vetenskap, och som biprodukt uppstår ännu en potentiell vinst av att använda matematik:

Det ser vetenskapligare ut.

Den här artikeln handlar om farorna med att glömma bort vad matematiken egentligen är till för och låta den kosmetiska biprodukten bli huvudsak. Då uppstår en sorts pseudomatematisk genre där matematiken finns med för sin egen skull. I stället för att bringa klarhet gör sådan matematik ofta framställningen mer svårgenomskådlig. Den ger gärna intryck av en precision som egentligen inte finns. Och inte sällan drar man i denna genre långtgående slutsatser om verkligheten från en illa underbyggd matematisk modell.

Pseudomatematik bland franska intellektuella

År 1996 blev fysikern och matematikern Alan Sokal världsberömd för att han lyckades få en parodi på postmodern rotvälska antagen och publicerad i en prestigefylld tidskrift. Året därpå gav han, tillsammans med sin kollega Jean Bricmont, ut en underbar bok om hur uppburna franska intellektuella ägnat sig åt pseudomatematiska skriverier.¹ Citaten är ofta lika pompösa som obskyra. Vad sägs till exempel om följande passage av Jacques Lacan, där han använder ekvationer för att utveckla ett psykoanalytiskt resonemang?

Med S= -1, fås s=√(-1). […] Därmed kommer det erektila organet att symbolisera platsen för extas, inte i sig själv, eller ens i form av en bild, utan som en del som saknas i den önskade bilden: det är därför som det är ekvivalent med √(-1) i signifikationen ovan, av den extas som den återställer genom koefficienten för dess påstående till funktionen av avsaknad av tecken (-1).²

Detta är mitt eget fåfänga försök till översättning från franskan. Jag erkänner glatt att jag själv inte begriper så mycket mer än att det manliga könsorganet påstås vara ekvivalent med ett imaginärt tal. En rätt dråplig jämförelse som man kan ha mycket roligt åt. Men ska man tolka Lacan som att han här skämtar och driver med sig själv? Knappast. Hela texten låter på samma sätt, och Lacans teorier om extas (jouissance) citeras ännu med största allvar inom genren.

Pseudomatematik bland svenska samhällsvetare

Sverige har ingen riktig motsvarighet till de franska intellektuella, men på Dagens Nyheters debattsida odlar svenska samhällsvetare en egen pseudomatematisk genre. Här följer tre exempel från 2000-talet som alla har ett speciellt mönster gemensamt:

Forskarna presenterar sina resultat på DN Debatt.
Någon annan forskare granskar på eget initiativ bakomliggande studie och formulerar allvarlig kritik i tidskriften Ekonomisk Debatt.
De ansvariga forskarna svarar på kritiken genom att angripa kritikern, varvid debatten avslutas.³

Ingen verkar ha uppmärksammat detta anmärkningsvärda mönster som jag ser som ett uppenbart problem i ett folkbildningsperspektiv. Eftersom mitt syfte är att belysa fenomenet, inte polemisera, så avstår jag från att nämna de kritiserade forskarna vid namn.

Äpplen och päron

Alla har hört att man inte ska blanda ihop äpplen och päron. Det är en metafor för att storheter inte är jämförbara om de inte har samma enhet. År 2000 skrev två professorer att de funnit att forskningsmedel ger störst samhällsekonomisk utdelning om de satsas i Stockholm. En annan professor, Sören Wibe, anade att grunden för denna slutsats var svag. Han granskade studien och fann att analysen byggde på addition av tal med olika enheter.

Hur kan någon få för sig att lägga ihop tal som har olika enheter? Jo, problemet som professorerna stod inför var att bedöma (den samhällsekonomiska) effekten av att satsa forskningspengar på en given ort. En sådan satsning borde ge effekt i form av arbetstillfällen inte bara på orten där forskningen sker utan även på andra orter. Professorerna antog att denna distanseffekt avtar med avståndet. Som modell antog de att följande samband gäller:
indirekt effekt = satsning/avstånd
Det är ett olyckligt val, ser du varför?

Problemet är vad effekten blir i den ort där satsningen sker. Där är ju avståndet från satsningen noll, men det går inte att dividera med noll! Istället antar professorerna att effekten på orten där satsningen sker helt enkelt är lika med satsningen.
direkt effekt = satsning
Då löser man ett problem men skapar ett annat. Satsningar mäts ju i kronor. Övriga effekter får enheten kronor per meter. När man summerar effekterna av satsningar i olika orter lägger man ihop termer som mäts i olika enheter. Sådana additioner ger meningslösa resultat.

Ett sätt att inse vidden av problematiken är att fundera på hur resultaten beror på valet av längdenhet. Det finns många avståndsmått här i världen, såsom meter, kilometer, mil och ljusår. I en riktig modell ska inte slutsatserna vara beroende av vilken enhet man råkar välja. Men titta vad som händer om man mäter i kilometer i stället för meter i modellen ovan: de termer som hör till direkta effekter förändras inte men alla andra termer i summan blir tusen gånger större!

Vad är ett samband?

Nästa exempel handlar om när man kan hävda att man har funnit ett orsakssamband. Ett positivt samband mellan två variabler är ett samband av typen ”mer av x ger mer av y”. Att ur data härleda och beskriva samband tillhör den tillämpade matematikens huvuduppgifter. Ofta gissar man att eventuella samband är linjära. Man beräknar därför den så kallade regressionslinje som passar bäst till datapunkterna och tittar på linjens lutning.

Figur 1 visar en datamängd där en linje med positiv lutning passar bra till de givna punkterna. Man kan då känna sig rätt övertygad om att det faktiskt finns ett allmänt positivt samband mellan x och y, även om man inte vet vad som orsakar vad.

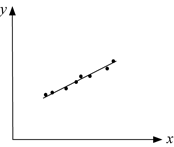
Figur 1. Punkter som tyder på ett positivt linjärt samband mellan x och y.

År 2001 kungjorde en rubrik på DN Debatt att Friskolor gynnar alla barn. Två ekonomer hade utfört en statistisk studie av sambandet mellan andelen friskolor i en kommun och elevernas betyg i den kommunala skolan. Deras slutsats var att sambandet var starkt och positivt. Ett samband mellan betyg och friskoletäthet skulle i och för sig kunna orsakas av en tredje variabel, såsom att kommuner med många friskolor har fler familjer med hög utbildningsnivå. Ekonomerna hade som tur var tillgång till data på flera sådana variabler som kunde tänkas vara av betydelse. Sambandet stod sig även när de försökte ta hänsyn till dessa variabler. De drog slutsatsen att konkurrensen från friskolor ökar kvaliteten i den kommunala skolan.

Man bör allmänt sett vara mycket försiktig med att dra slutsatser om orsakssamband när man inte kan hålla precis alla förutsättningar lika. Hur kan man veta att sambandet inte beror på ytterligare någon variabel som man inte har tänkt på? Ekonomernas metod hade dock ett mer grundläggande problem, och återigen var det Sören Wibe som gjorde granskningen. Titta på figur 2.

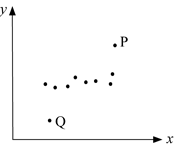
Figur 2. Punkter som inte tyder på något särskilt samband mellan x och y. Två avvikare, P och Q, gör att regressionslinjen ändå får positiv lutning.

Figur 2 visar en tänkt situation där den bästa linjen inte alls passar särskilt bra till data. Regressionslinjens lutning tyder visserligen på ett positivt samband, men ögat låter sig inte övertygas – hela lutningen beror ju på punkterna P och Q! Tar man bort de två punkterna återstår inget positivt samband mellan x och y. Dessa data tyder inte på att mer av x ger mer av y i allmänhet. I stället verkar det vara något särskilt med P och Q.

Sören Wibe undersökte vad som hände om han tog bort några orter från studiens urval av 33 kommuner. Han fann då att sambandet försvann om Pajala och Göteborg togs bort. Situationen liknade alltså den i Figur 2. Som Wibe konstaterar, om det verkligen funnes ett orsakssamband mellan friskolor och goda betyg så borde det synas oavsett om Pajala och Göteborg är med i urvalet eller inte.

En stor del av sitt svar ägnar ekonomerna åt en egen ”systematisk” robusthetsanalys. Till exempel provar de i sin modell att ta bort kommuner ur urvalet på olika sätt. De finner då att sambandet mellan betyg och friskolor kvarstår för alla utom ett litet fåtal av de många möjligheter som finns att ta bort två av 33 kommuner. Deras slutsats av denna övning är att ”resultaten är robusta”. Detta är hemgjord nonsensmatematik. Om sambandet försvinner när två datapunkter tas bort, då är det ju inte robust. Att ett skenbart samband kvarstår vid de flesta andra sätt att plocka bort datapunkter är självklart, det är bara att se på Figur 2. De flesta par av datapunkter stödjer ju inte det påstådda sambandet, och när sådana par tas bort finns givetvis det skenbara sambandet kvar.

Okänd skala

Mitt tredje exempel handlar om okända enheter. Anta att någon erbjuder dig att delta i ett internationellt lotteri där vinstbeloppen sägs vara 100, 200, 500, 1000, 5000 och 25000. ”Ursäkta, 25000 vad?”, undrar du. Kronor, dollar, euro, pund, yen? Det går naturligtvis inte att enbart från beloppen säga vilken valuta de beskriver.

År 2004 skrev en svensk sociolog på DN Debatt under rubriken Kön skäl för löneskillnad. Tillsammans med en amerikansk kollega hade hon funnit något anmärkningsvärt: MBA-studenter, både i Sverige och USA, anser att könet på en verkställande direktör spelar stor roll för vilken lön direktören bör ha. Allt annat lika ansåg studenterna att det vore rättvist att en kvinna har 15 procent lägre lön än en man. När jag själv granskade studien fann jag att forskarnas metod för att ta reda på MBA-studenternas ”sanna” uppfattningar var mycket speciell. Studenterna ombads nämligen ange orättvisan i olika löneförslag som ett tal på en personlig godtycklig skala . En student säger att orättvisan på hennes skala är ”17”. En annan student säger att orättvisan på hans skala är ”3000”. Vi vet inget om hur skalorna förhåller sig till varandra. Det är alltså samma sorts situation som i lotteriexemplet ovan.

Anta att någon har svarat ”A:s lön på tio miljoner dollar är 500 orättviseenheter för låg, B:s lön på två miljoner dollar är 65 orättviseenheter för hög”. Utgående från detta svar vill vi räkna ut vad de rättvisa lönerna är. Men vi har inte en aning om vilken skala respondenten har använt. Om vi hade vetat vad respondenten anser vara rättvist skulle vi kunna räkna fram skalan baklänges, men tvärtom är det just vad respondenten anser vara rättvist som vi vill forska fram. Det är en logisk omöjlighet att enbart från en uppsättning tal veta vilken enhet de betecknar. De två sociologerna verkar dock tro att matematik kan uträtta underverk. De sätter upp ett antal matematiska formler som ser mycket imponerande ut, se själva i Figur 3! Genom att köra svaren genom dessa formler menar de att de får ut sanningen om vad respondenten egentligen menade med sin godtyckliga skala.

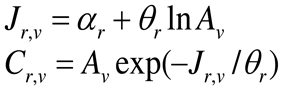
Figur 3. Matematiska formler som enligt artikelförfattaren ger ett imponerande intryck.

Vad får då forskarna för resultat med sin metod? I DN-artikeln berättade de att de funnit en genomsnittlig skillnad på 15 % mellan rättvisa löner på män och kvinnor. Men genomsnitt är bara intressanta om de beräknas på vettiga värden. De underliggande värdena stod inte i DN, men de finns i en tabell i forskarnas rapport. Där kan man se vad de med sin metod har räknat ut att folk tycker. Enligt forskarna finns det en student som anser att – håll i er nu – 1430000000000000000000000000000 dollar om året vore en rättvis lön för en viss VD. Jacques Lacans påstående om att det manliga könsorganet är ekvivalent med roten ur minus ett framstår i jämförelse som ganska rimligt.

Kritiker måste det vara något fel på

Ovan har jag för varje studie bara refererat en enstaka logisk brist. I samtliga exempel pekade kritikerna i själva verket ut flera olika allvarliga problem. Hur reagerar man då inför sådan konkret kritik? Hur skulle en riktig matematiker reagera? Det händer givetvis ganska ofta att även vi, särskilt jag själv, gör logiska fel. I allmänhet upptäcks sådana fel på ett tidigt skede, av en själv eller i samtal med intresserade kolleger. Nästa filter är peer review-processen i den vetenskapliga tidskrift man skickar resultaten till. (Matematiker publicerar nämligen aldrig sin forskning på DN Debatt.) Oavsett i vilket skede ett fel upptäcks så rodnar författaren och rättar till studien eller drar tillbaka den.

Skillanden mot reaktionerna på Sokal och Bricmonts bok kunde inte vara större. De franska intellektuellas typiska reaktion var inte ”Usch, har vi skrivit sådana dumheter?” utan ”Sokal och Bricmont är fascister”.

Var på skalan mellan dessa båda extremer lägger sig då de svenska pseudomatematikerna? Min bedömning är att de helhjärtat ansluter sig till den franska skolan. Inte i något fall görs någon ansats till självkritik. Redan de rubriker som forskarna har valt på sina genmälen illustrerar devisen ”anfall är bästa försvar”.

Professorerna med forskningssatsningarna kallar sin replik Rekviem över en granskningsrapport. Angående enhetsproblematiken skriver de att enheten de använt för avstånd var kilometer, ”men att det inte spelar någon roll så länge som alla avstånd mäts i samma enhet.” Detta är, som vi sett, fel. Inte ens efter att ha läst kritiken har alltså dessa professorer brytt sig om att reda ut egenskaperna hos den egna matematiska modellen. Slutklämmen i genmälet är att ”Sören Wibe försöker strypa en öppen debatt”. Vi andra tycker nog att Wibe försöker föra en vetenskaplig debatt.

Repliken från de två ekonomerna heter Wibes kritik är grundlös! Under delrubriker som ”Wibes vantolkningar” och ”Wibes undermåliga analys” ägnar forskarna nio sidor åt att tala om varför det är Sören Wibe och inte deras modell som förtjänar kritik. Angående att Wibe funnit att resultaten inte var robusta skriver de: ”[A]lla som hållit på med en statistisk analys vet hur lätt det går att inte finna ett signifikant samband om man bestämmer sig för det”. Detta är nonsens. Alla som hållit på med statistisk analys borde veta att det är den som förespråkar ett samband som har bevisbördan.

De två sociologerna som jag själv kritiserade kallar sitt svar Entydigt felaktiga påståenden. De syftar tyvärr inte på sina egna påståenden. I svaret skriver de bland annat: ”Ett annat oriktigt påstående som Eriksson gör är att det är omöjligt att skatta den respondent-specifika skalfaktorn. Tvärtom, denna faktor är en viktig ingrediens i den indirekta metoden för skattning av Just Pay.” Men att det är viktigt att kunna göra en sak betyder tyvärr inte att det faktiskt går att göra. Är det viktigt för metoden så är det tvärtom bara desto allvarligare att det inte låter sig göras! Om den trettiosiffriga lönen skriver sociologerna vidare: ”[B]ara för att Eriksson uppfattar skattningarna av Just Pay som orimliga betyder inte detta att skattningarna är orimliga.” Forskarna hyser alltså så stark tilltro till sin matematiska metod att den inte rubbas ens av helt groteska resultat. Med en kvintiljon dollar i årslön till VD kommer även det mest kapitalstarka företaget i världen att vara bankrutt redan en bråkdel av en sekund efter det att anställningskontraktet skrivits under. Vem skulle anse att det är rättvist?

Sammanfattning

Jag har visat på ett mönster där vissa svenska samhällsvetare ägnar sig åt hemgjord pseudomatematik. Varför gör de på detta viset? Det här är min förklaringsmodell: jämfört med naturvetenskapen är det vanligt att samhällsfenomen är mer komplicerade att analysera samtidigt som forskarna ofta har mindre matematik i sin utbildning. Vetskapen om att matematiken är kraftfull och prestigefull lockar dem att använda avancerade modeller vars detaljer de inte själva begriper, och hitta på hemgjorda metoder som ofta bygger på missuppfattningar. I brist på förståelse måste man tro, och tro är mycket svårare att rubba. De orimligt starka slutsatser som den troende drar håller hon eller han sedan fast vid även när kritiker påpekar allvarliga brister. Instinkten säger att det måste vara kritikern det är fel på.

Extra svårt blir det förstås att ta in nya synpunkter när debatten sker offentligt. Detta är den kanske allvarligaste invändningen mot att forskare publicerar sina resultat som debattartiklar i dagspressen. Om man ser till att erhålla kritiska vetenskapliga synpunkter innan man går ut med resultaten i pressen är det inte alls lika svårt att svälja prestigen. Men den som blir kritiserad offentligt känner sig gärna orättvist uthängd och illa behandlad, hur giltiga synpunkter kritikern än har.

Den här artikeln har handlat om matematikens baksida – om dess kännetecken, hur man ska förstå den, och helst även se det komiska i den. Låt mig åter påminna om att det finns en framsida också. Rätt väg att gå inom samhällsvetenskapen är absolut inte att sluta använda matematik, utan att avdramatisera den. Den är varken farlig eller fin – den är användbar. Kompetenta, och därför respektlösa, användare finns det gott om både inom och utom fältet; den som känner sig osäker har många att fråga.

En avdramatisering av matematiken innebär också att man inte sätter den matematiska modellen främst, utan låter verkligheten få sista ordet. Ta till exempel de rättvisa lönenivåer som de två sociologerna räknat fram. Dessa lönenivåer kunde de ha testat direkt mot respondenterna – om metoden fungerar ska ju respondenterna nu ange att orättvisan är noll!

Eller ta ekonomernas friskoleeffekt. Om den existerar bör den kunna observeras även på andra sätt, till exempel genom att kommuner som över tid får fler friskolor också får högre betyg. Wibe gjorde en egen analys av detta och fann ingen sådan effekt. Denna väsentliga poäng lämnades helt utan kommentar av ekonomerna i deras genmäle, vilket för in på mitt sista tema: bättre rutiner för hur tidningar och tidskrifter ska förhålla sig till vetenskapliga debatter.

Om slutsatserna i en vetenskaplig studie möter kritik är det oansvarigt av redaktörer att ta in genmälen som inte behandlar de kritiska punkterna seriöst. Läsare som inte själva är experter lämnas med en känsla av att inte veta vare sig ut eller in. En nackdel med matematiska spörsmål är att debatten lätt blir teknisk. Om redaktören själv inte känner sig kompetent att avgöra vad som är rätt eller fel finns oberoende experter att fråga – en fördel med matematiska spörsmål är ju att det oftast finns rätt och fel. Varför inte försöka få det lite mindre fel och lite mera rätt? Tidningarna har ju språkgranskare; fram för siffergranskare!⁴

Noter

Alan Sokal och Jean Bricmont, Impostures Intellectuelles (1999).
Jacques Lacan, Ecrits (1966), s. 822.
De tre debatterna återfinns i Ekonomisk Debatt 7/2000, 3/2002 och 2/2005. Enstaka utvalda citat gör förstås ingendera sidan full rättvisa. Nyfikna läsare uppmuntras att ta del av debatterna i sin helhet.
Idén kommer från Sten Kaijser, f.d. ordförande i Svenska Matematikersamfundet.